Understanding diff algorithms

Programmers spend a lot of time looking at diffs. For example, when we get an error like expected 'aabbeeccdd' but got 'aabbeeecdd', we don’t squint at the screen, we run a diff tool - a program that shows:

However, many programmers don’t have a good understanding of how their diff tool works. When I talk to people about the webapp that I made, diffdiff.net, they ask (with a raised eyebrow) “did you write the core algorithm yourself?”

I did! It was one of the easiest parts of the whole thing! It was WAY easier, for example, than getting the dialog box to animate away properly. However, while reading about how to implement the algorithm, I didn’t find an explanation that emphasized just how simple this algorithm is. My goal with this article is to write the explanation I wish I’d found.

Input and Output

First, let’s define the input and output of the algorithm. The input is two versions of a file, before:

1#include <stdio.h>
2int main() {
3  printf("Hello!");
4}

And after:

1#include <stdio.h>
2#include <html.h>
3#include <styles.h>
4int main() {
5  write(bold("Hello"));
6}

A side-by-side diff makes it easy to see the difference between these two files:

1	#include <stdio.h>	1	#include <stdio.h>
		2	#include <html.h>
		3	#include <styles.h>
2	int main() {	4	int main() {
3	printf("Hello");
		5	write(bold("Hello"));
4	}	6	}

(You can scroll the diff views if they don't fit on your screen)

A view like this is what we want to generate.

Looking closely at this example indicates the input and output we need. As input, we take two lists of lines:

 1before = [
 2  '#include <stdio.h>'
 3  'int main() {'
 4  '   printf("Hello");'
 5  '}'
 6]
 7
 8after = [
 9  '#include <stdio.h>'
10  '#include <html.h>'
11  '#include <styles.h>'
12  'int main() {'
13  '   write(bold("Hello"));'
14  '}'
15]

As output, we need a list of pairs {before, after}. The before element of the pair is the index of a line in before, the after element of the pair is the index of a line in after. If the lines aren’t the same, then either pair.before or pair.after is null.

Another way of thinking about this is the line numbers on the side-by-side diff, with blank represented by null.

before		after
1	#include <stdio.h>	1	#include <stdio.h>
null		2	#include <html.h>
null		3	#include <styles.h>
2	int main() {	4	int main() {
3	printf("Hello");	null
null		5	write(bold("Hello"));
4	}	6	}

So the actual object that our algorithm will return will be:

 1diff = [
 2  // #include <stdio.h> - in both
 3  {before:0, after:0},
 4
 5  // #include <html.h> - only in 'after'
 6  {before:null, after: 1},
 7
 8  // #include <styles.h> - only in 'after'
 9  {before:null, after: 2},
10
11  // int main() { - in both
12  {before: 1, after: 3},
13
14  //   printf("Hello"); - only in 'before'
15  {before: 2, after: null},
16
17  //    write(bold("Hello")); - only in 'after'
18  {before: null, after: 4},
19
20  // } - in both
21  {before: 3, after: 5},
22]

This list of pairs will let us display the diff any way we want. For example, the code that generated the HTML above is essentially:

 1function print(diff) {
 2  // helper function
 3  const addChild = (el, tag) =>
 4      el.appendChild(document.createElement(tag));
 5
 6  const table = document.createElement('table');
 7  for (pair of diff) {
 8    const row = addChild(table, 'tr');
 9
10    const beforeCell = addChild(row, 'td');
11    beforeCell.textContent =
12        pair.before === null ? '' : pair.before;
13
14    const afterCell = addChild(row, 'td');
15    afterCell.textContent =
16        pair.after === null ? '' : pair.after;
17  }
18  document.body.appendChild(table);
19}

Rules

A list of pairs is the data structure we need to display diffs, but not just any list of pairs will do! There are three important rules that the output needs to follow:

Match up as many lines as possible. It’s just not useful to show a diff like this:

1	#include <stdio.h>
2	int main() {
3	printf("Hello");
4	}
		1	#include <stdio.h>
		2	#include <html.h>
		3	#include <styles.h>
		4	int main() {
		5	write(bold("Hello"));
		6	}

Match up only identical lines. It would be super confusing and unhelpful to show a diff that matches up lines that are not the same. It makes it look like the algorithm didn’t detect a change (like line 3 / 5 below):

1	#include <stdio.h>	1	#include <stdio.h>
		2	#include <html.h>
		3	#include <styles.h>
2	int main() {	4	int main() {
3	printf("Hello");	5	write(bold("Hello"));
4	}	6	}

Keep the lines in the same order. If your diff program showed you this diff, with the lines jumbled up, you would not be happy:

1	int main() {	1	int main() {
2	#include <stdio.h>	2	#include <stdio.h>
3	}	3	}
4	printf("Hello");
		4	#include <html.h>
		5	#include <styles.h>
		6	write(bold("Hello"));

What we want, in fancier terms, is the “maximum common subsequence”:

“Maximum” = align as many as possible
“common” = of the identical lines
“subsequence” = without reshuffling the lists

The algorithm

The key to solving this problem is to think about it in a different way: surprisingly, the way to find the maximum common subsequence is to find a shortest path!

Write the before text horizontally and the after text vertically. We’re going to treat pairs of lines like nodes and edges in a graph, so connect every node to the nodes below it and to the right. This is like a map of a (very regular) city:

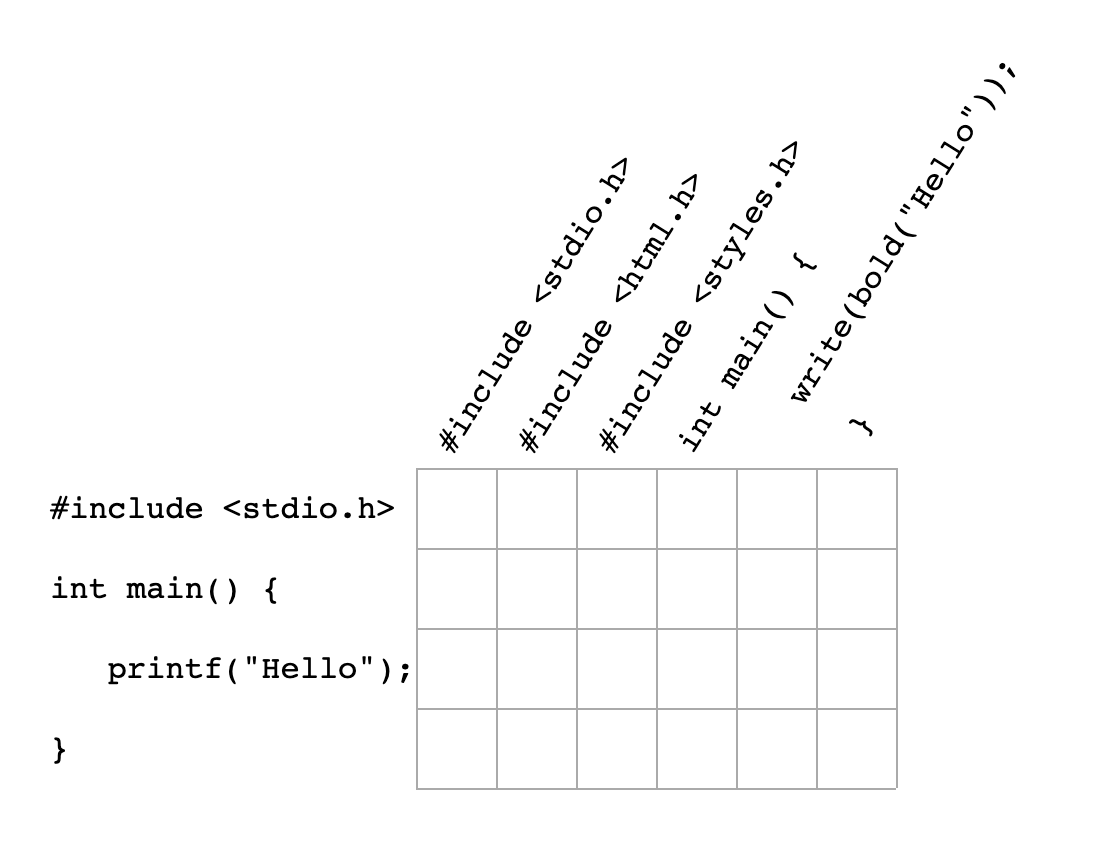
Then, if the lines of text are the same, make a diagonal connection down and to the right. This is like a shortcut through a city block:

The thing we’re looking for, the maximum common subsequence, corresponds exactly to the shortest path from the top-left to the bottom-right of this network! Take a look:

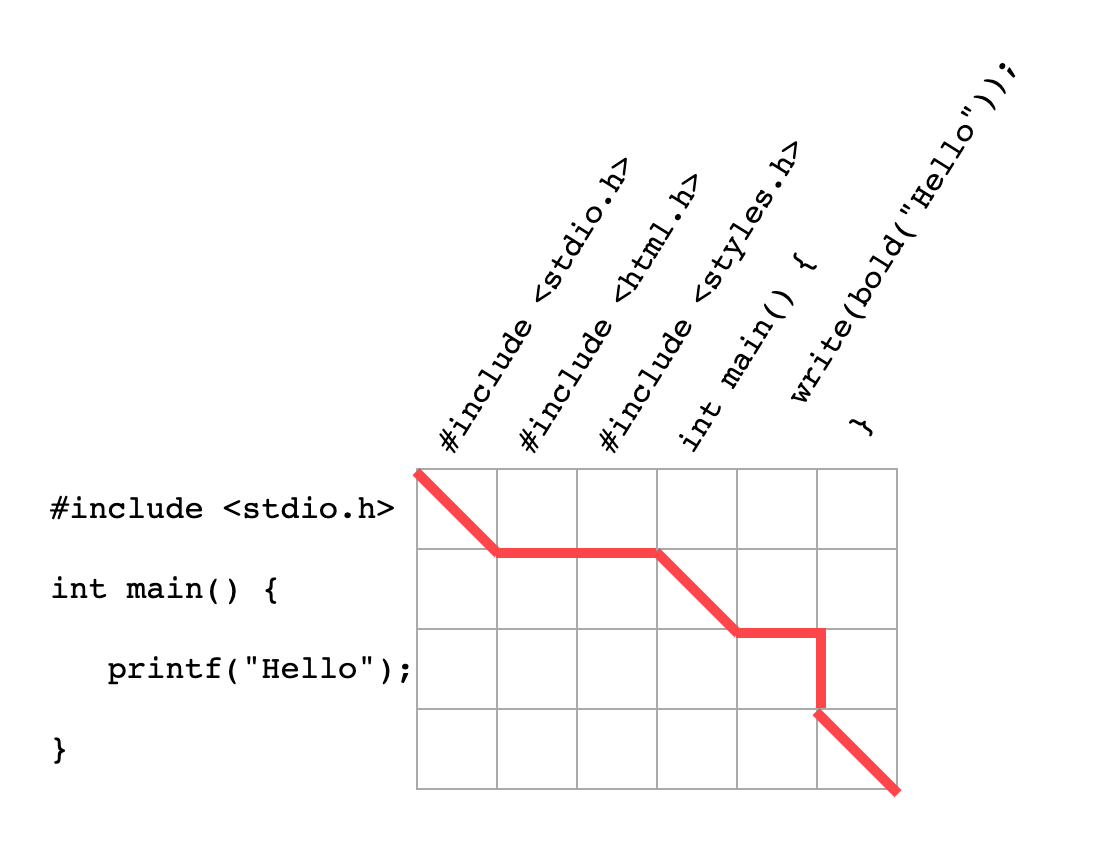
Diagonal connections indicate matching pairs (like #include <stdio.h> on line 1)
Horizontal connections indicate a new line in after (like #include <html.h> on line 2)
Vertical connections indicate a deleted line in before (like printf("Hello"); on line 3)

The shortest path uses the maximum number of shortcuts. Every shortcut represents a matching pair. So the shortest path represents the maximum number of matching pairs!

Now any shortest-path algorithm will work to solve the problem! Take, for example, Dijkstra’s algorithm. Dijkstra’s algorithm works by “visiting” nodes further and further from the source node until it finds the destination node. Here it is at work in our graph:

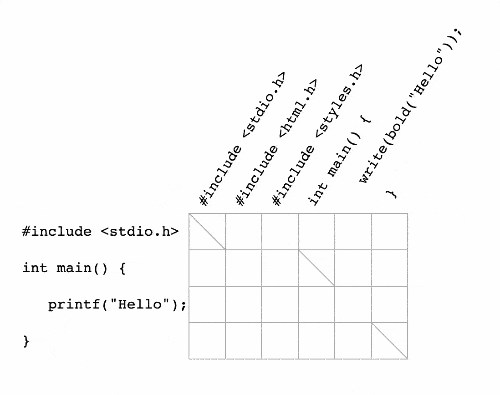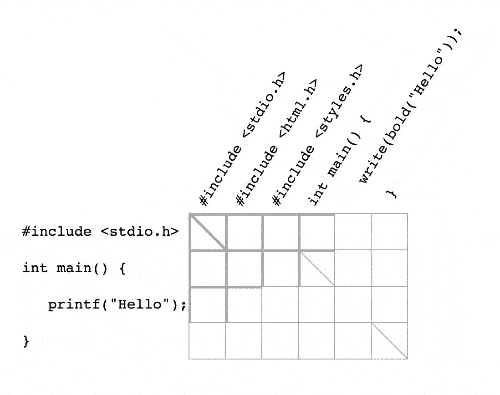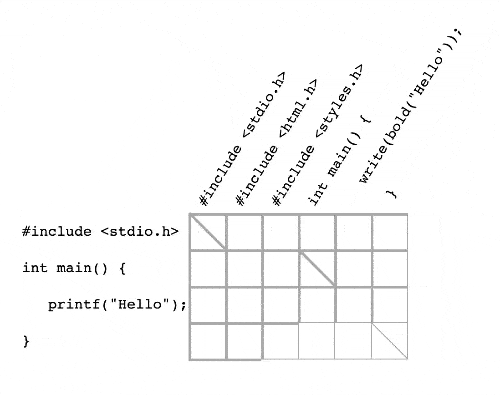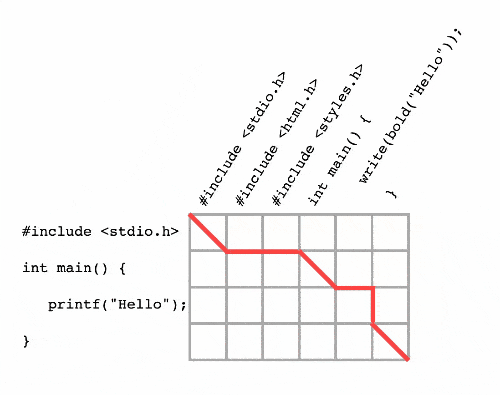
Dijkstra’s algorithm is a diff algorithm! However, you might notice that it seems to be doing a lot of extra work - what is the point of exploring nodes in the bottom-left of our graph when we could be exploring closer to the destination node? That’s an acute observation - Dijkstra’s algorithm works on any graph, but we can use algorithms that are more specialized for our graph.